简介

这里是一个对于常见过滤器及其变体的总结，目前包括：

为什么我们需要过滤器？多数情况下是因为我们没办法处理所有的数据，需要一些近似的手段保存和记录数据。尤其是在交换机上，不仅能调配的资源十分有限，需要处理的流量也极大。我们不得不使用各种过滤器搭建数据面 Sketch 记录和保存我们所需数据某个聚合（当然也可以动态地由控制面调节具体参数），否则交换机本身、通信链路都无能处理。

在使用过滤器时，最朴素的用法是：定义好桶（cell）的字段，直接按需收集信息。常见的优化方式包括：在 Ingress 和 Egress 分别部署两个过滤器，通过分析过滤器差值得到数据（如丢包）；在字段中使用 XOR 以满足可逆性；在过滤器之前前置一个 Bloom Filter，确保流入过滤器的数据严格不重……我们并不要求过滤器得到的结果严格正确，但一般只允许出现 negl 概率的假阳性（例如 Bloom Filter），而不允许出现错阴性，这视具体任务要求而定。

Bloom Filter

BF 用于维护一个支持：插入元素、查找存在性的集合。

一个 BF 包括 $n$ 个 cell 和 $m$ 个 Hash 函数，分别记为 $c_i$ 和 $h_i$。插入键值 $k$ 时，将 $c_{h_i(k)}$ 的值置为 $1$，即将 $k$ 通过 $m$ 个 Hash 函数算出 $m$ 个下标，并将这些下标对应的桶置 $1$。查找存在性时返回 $\prod_{i=1}^m c_{h_i(k)}$ ，即是否该元素所有对应的桶都为 $1$。

BF 会有假阳性，但不会有错阴性。假设用于存储 $N$ 个不同元素，则等价于在 $n$ 个 cell 中随机置 $1$ 操作 $Nm$ 次，因此单个元素为 $0$ 的概率为 $p=(1-1/n)^{Nm}$。于是假阳率为：$P_{fp}=(1-p)^m\approx (1-e^{-Nm/n})^m$。一般使用时，$N$ 和 $n$ 是已知量，给定 $P_{fp}$ 的可接受上界反推 $m$。

Invertible Bloom Lookup Table

IBLT 在 BF 的基础上，将存在性查找拓展为键值对存储。支持：插入键值对、删除键、根据键查找值。

一个 IBLT 包括 $n$ 个 cell 和 $k$ 个 Hash 函数，分别记为 $c_i$ 和 $h_i$。额外注意：IBLT 要求 $h_i$ 不产生重复结果，这可以通过将 $n$ 个 cell 划分为 $k$ 个 $n/k$ 的 cell 组合做到，且不影响渐进复杂度。每个 cell 包含 3 个字段：count、keySum、valueSum，初始均为 $0$。IBLT 会前置一个 BF，用于检验对应键是否已经被插入到 IBLT 中，确保 IBLT 维护的键是一个不可重集合。

与 BF 类似，下文将一个键 $k$ 对应的所有下标的 cell 称为 “对应 cell”。

  • 插入键值对 $(K,V)$：将所有对应 cell 的 count += 1, keySum += K, valueSum += V
  • 删除键值对 $(K,V)$：将所有对应 cell 的 count -= 1, keySum -= K, valueSum -= V
  • 查找键 $K$ 对应的值：
    • （Fast Path）先遍历所有对应 cell，看看有没有满足：count == 1 && keySum == K 的，如果有就返回对应 value；如果发现 count == 0 或者 count == 1 && keySum != K 的，则为键 $K$ 不存在
    • （Slow Path）若找不到，则尝试全量解码：不断尝试找到一个满足 count == 1 的桶（称为纯桶），拿取其中的 (keySum, valueSum) 作为键值对，执行删除键值对。直到能够找到一个桶满足 count == 1 && keySum == K 则成功，或者无法继续删桶则失败

实际上 keySum 和 valueSum 的维护一般使用 XOR 异或和，确保操作的可逆性和值域范围。

全量解码的过程等价于对一个随机 $m-$超图进行 peeling，即反复删除度数为 $1$ 的点及其关联的超边，该问题有解当且仅当图中不存在 2-core。结论是：存在一个常数 $C$，当 $N>Cn$ 时解码几乎总是失败，当 $N<Cn$ 时解码几乎总是成功；其中 $C=\sup{0<\alpha<1;\forall x\in(0,1),1-e^{-k\alpha x^{k-1}}<x}$。当 $k=3$ 时取到最大值约 $0.818$，即需要约 $1.222$ 倍于元素数量的桶即可确保解码的高成功率。

感谢 2e19728 提供的计算结果：当 $k$ 不限于自然数时，当 $k\approx3.0077$ 时取到最大值

注意到上述分析是针对 IBLT 本身的无解概率，还需要额外考虑前置 BF 的假阳率和假阳带来的影响。

为什么使用 IBLT：直观上看，IBLT 只能存储 $0.818$ 倍总桶数个元素，那为什么我不直接开一个线性表存储呢？一方面是 IBLT 方便 Hash 进行 $O(1)$ 寻桶，另一方面是 IBLT 对合并的支持很好，两张键相同的 IBLT 可以直接求并、求差，水平扩展性很好。

Count-Min Sketch

CMS 用于统计键出现的频数，支持：插入键、查找键频数。

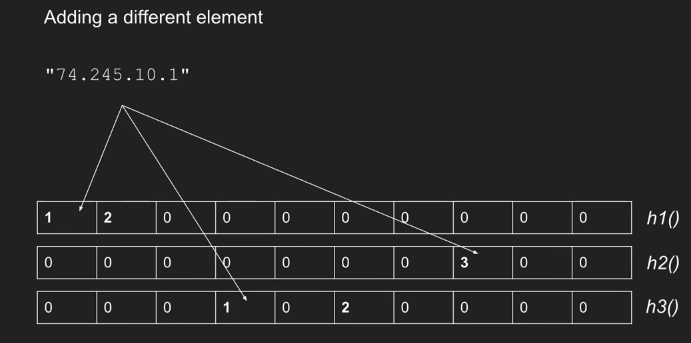
一张 CMS 包含 $k$ 个 Hash 函数（记为 $h_i$）和一张 $k\times W$ 的频数表 $S$。在插入键 $K$ 时，将 $S[i,h_i(K)],i\in[1,m]$ 的值增加 $1$；在查找键 $K$ 的频数时，返回 $\min_{i\in[1,m]}S[i,h_i(K)]$。即直接查找对应格子的频数最小值。

CMS 也有假阳性问题，查询到的值大于等于实际频数。结论是：若元素个数为 $N$，我们要满足对任意元素 $k$ 都以至少 $1-\delta$ 的概率有 $f’(k)\leq f(k)+\epsilon N$ 的条件下，需要有 $W=\lceil e/\epsilon \rceil,k=\lceil \ln(1/\delta)\rceil$。并且，CMS 的假阳性问题会在出现大象流时更加严重：一个大象流可能会严重影响恰好与其碰撞的几个小流的估计值。

Cuckoo Sketch

Cuckoo Hash 是一种键存储方案，作用类似于 BF；保证不会出现假阳性，但可能出现假阴性（插入时也会对假阴性报错）。思想为：准备两个 Hash 函数 $h_1$ 和 $h_2$，待存储的键 $k$ 一定存在于 $C_{h_1(k)}$ 或者 $C_{h_2(k)}$ 中。若这两个 cell 都被使用，则先插入其中一个，把那个 cell 原本存储的键踢出，然后不断尝试将多出来的键插入到他另一个对应的 cell 中，直到遇到一个空 cell。

考虑建图 $G$：点为 cell，当两个 cell 能够同时对应到一个元素时联边。插入过程无解当且仅当图 $G$ 中形成了一个环，即 IBLT 分析中的 2-core 问题的普通图版本（$k=2$）。取 $k=2$ 时，得到负载因子 $C=0.5$。

Cuckoo Filter 是对 Cuckoo Hash 的改进，优化了内存占用，不必存储完整的键且支持删除。Cuckoo Filter 只需要定义一个 Hash 函数，记为 $H$；则有 $h_1(x)=H(x),h_2(x)=H(x)\oplus H(\phi(x))$。其中 $\phi(x)$ 是 $x$ 的指纹函数，也是记录到 cell 中的值。由于有 $h_1(x)\oplus h_2(x)=H(\phi(x))$，我们在踢出 $i$ 号 cell 中的元素 $V$ 时，可以推算出：它的另一个备选位置位于 $H(V)\oplus i$。

由于 Cuckoo Filter 中 $h_1,h_2$ 不再独立，因此对 Cuckoo Filter 的 Balance 分析不再适用。（但差距不大）

Augmented Sketch

Augmented Sketch 基于 CMS，是为了解决部分大流对假阳性的严重影响而设计的。其大致思路是：维护一个 CMS 和一个精确的 Table，CMS 负责记录小流，Table 负责记录大流。

当需要插入一个键 $(k,u)$ 时，Augmented Sketch 首先尝试在 Table 中查找 $T[k]$，如果找到则直接更新；如果没找到但 $T$ 未满则直接插入；否则去更新 CMS。当更新完 CMS 之后，我们判断 $CMS[k]$ 是否已经超过了 Table 中频数最小的那一项（设为 $T[m]=l$）。如果是，则需要将两者互换位置：

  • 在 Table 中插入 $(k,CMS[k])$
  • 在 CMS 中插入 $(m,l-l’)$，其中 $l’$ 是上次将 $m$ 从 CMS 置换到 Table 时，$CMS[m]$ 的值（这保证了 CMS 中对 $m$ 统计的频数是正确的）

由于我们并没有在置换时，将 $k$ 在 CMS 中已记录的值删去，因此 Augmented Sketch 在 CMS 的基础上又会额外引入一定 Overestimate。但鉴于 CMS 本身也是 Overestimate 的，所以确保了整个系统也是 Overestimate 的。

Fermat Sketch

Fermat Sketch 在 ChameleMon 中提出，是 IBLT 的改进版。由于 IBLT 仅仅是一个数学上的模型，在实际部署和实现时，会遇到 $keySum$ 字段爆空间的问题（你可以轻松计算 $valueSum$ 的值域，但是 $keySum$ 一般都非常大，可能单独一个 $key$ 就需要 uint64_t 存储了）。Fermat Sketch 在 IBLT 的基础上支持了自然溢出后，IBLT 的插入和查询。

具体的改动只有一处：我们选定一个大质数 $P$（需要大于所有可能的 $key$），并在存储时直接对 $P$ 取模做加法。在查询时，如果我们遇到了一个只存储过一个键的桶，那么一定会有 $(count\times key)\mod P=keySum$。由费马小定理，两边同乘 $count^{P-2}$ 即可还原出 $key$。剩余步骤与 IBLT 相同。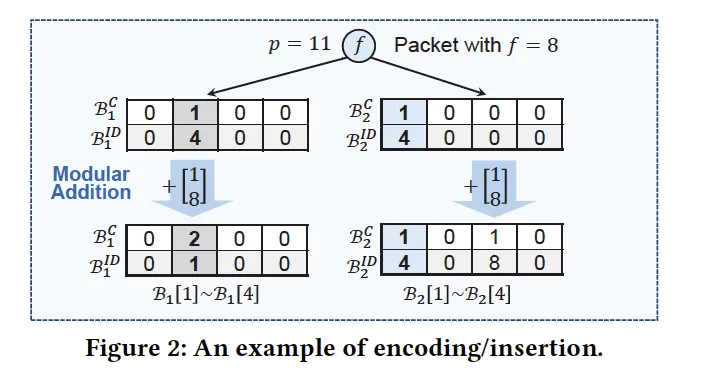

HyperLogLog

HyperLogLog 用于估算一批数据中不重复的元素个数。

HyperLogLog 基于伯努利估计，外加了分桶机制降低误差。基本思想是：统计所有数据中最长前导零的个数，平均 $2^K$ 个不重复元素会产生一个前导零长度至少为 $K$ 的数据。因此最朴素的想法是：统计 $L=\max {\text{前导零}}$，则估计共出现了 $2^L$ 个不同的元素。

在此基础上，HyperLogLog 为了降低估计误差，将数据按前 $B$ 位分桶（共有 $m=2^B$ 个桶），每个桶内分别统计最长前导零长度（记为 $R_i$）；则计算所有桶估计结果的调和平均，得到估计值 $N_{HyperLogLog}=(\alpha_m\times m^2)/(\sum_{i\in[0,m)}2^{-R_i})$，其中 $\alpha_m=(\int_0^{+\infty}(\log_2 \frac{u+2}{u+1})^m\text{d}u)^{-1}$（近似估计：$\alpha_{16}=0.673,\alpha_{32}=0.697,\alpha_{64}=0.709,\alpha_{m(m\geq128)}0.7213/(1+1.079/m)$，该估计引用了 数学人生-知乎）。